Inferring Galactic Structure from a Billion Stellar Colors

Gregory Green, Edward Schlafly & Douglas Finkbeiner

Pan-STARRS 1

$grizy$ photometry
Covers entire sky north of $\delta = -30^{\circ}$

2MASS

$J H K_s$ photometry
Full-sky

~800 million stars with high-quality, multi-band photometry

Problem Statement

Pixelization

Assume all stars in one pixel trace the same reddening column

Model Parameters

$\hphantom{\mu_{k} ,\,} \Delta E_{j} ,$	$\ \ j = 1, \ldots , n_{\mathrm{bins}}$
$\mu_{k} ,\,$ $\delta_{k} ,\,$ $\Theta_{k} ,$	$\ \ k = 1, \ldots , n_{\mathrm{stars}}$

$$ \left. \vphantom{ \begin{align} \Delta E_{j} \\ \Theta_{k} \\ \Theta_{k} \end{align} } \right\} \Rightarrow \vec{m}_{k} $$

Factorizing the Problem

$p \left( \left\{ \Delta E \right\} | \left\{ \vec{m} \right\} \right)$ $\propto p \left( \left\{ \Delta E \right\} \right)$ $\prod_{k}$ $\int$ $\mathrm{d} \mu_{k}$ $\mathrm{d} \Theta_{k}$ $\mathrm{d} \delta_{k}$ $p \left( \vec{m}_{k} \, | \, \mu_{k} , \Theta_{k} , \left\{ \Delta E \right\} , \delta_{k} \right)$

$\times \ p \left( \mu_{k} , \Theta_{k}, \delta_{k} \, | \, \left\{ \Delta E \right\} \right)$

For each star, pre-compute

$\tilde{p} \left( \mu_{k} , E \, | \, \vec{m}_{k} \right) = $ $\int \mathrm{d} \delta_{k}$ $\int \mathrm{d} \Theta_{k}$ $p \left( \mu_{k} , \Theta_{k} , \vphantom{\left( 1 + \delta_{k} \right)} \right.$ $\left( 1 + \delta_{k} \right)$ $\left. E \, | \, \vec{m}_{k} \right)$ $p \left( \delta_{k} \, | \, E \right)$

Then sample the line of sight

$p \left( \left\{ \Delta E \right\} | \left\{ \vec{m} \right\} \right)$ $\propto p \left( \left\{ \Delta E \right\} \right)$ $\prod_{k}$ $\int \mathrm{d} \mu_{k}$ $\tilde{p} \left( \mu_{k} , E \left( \mu_{k} , \left\{ \Delta E \right\} \right) | \, \vec{m}_{k} \right)$

$\hphantom{p \left( \left\{ \Delta E \right\} | \left\{ \vec{m} \right\} \right) \propto p \left( \left\{ \Delta E \right\} \right) \prod_{k} \int \mathrm{d} \mu_{k} \ } \underbrace{\hphantom{ \tilde{p} \left( \mu_{k} , E \left( \mu_{k} , \left\{ \Delta E \right\} \right) | \, \vec{m}_{k} \right) }}_{\mathrm{pre-computed}}$

Line integral through stellar probability densities

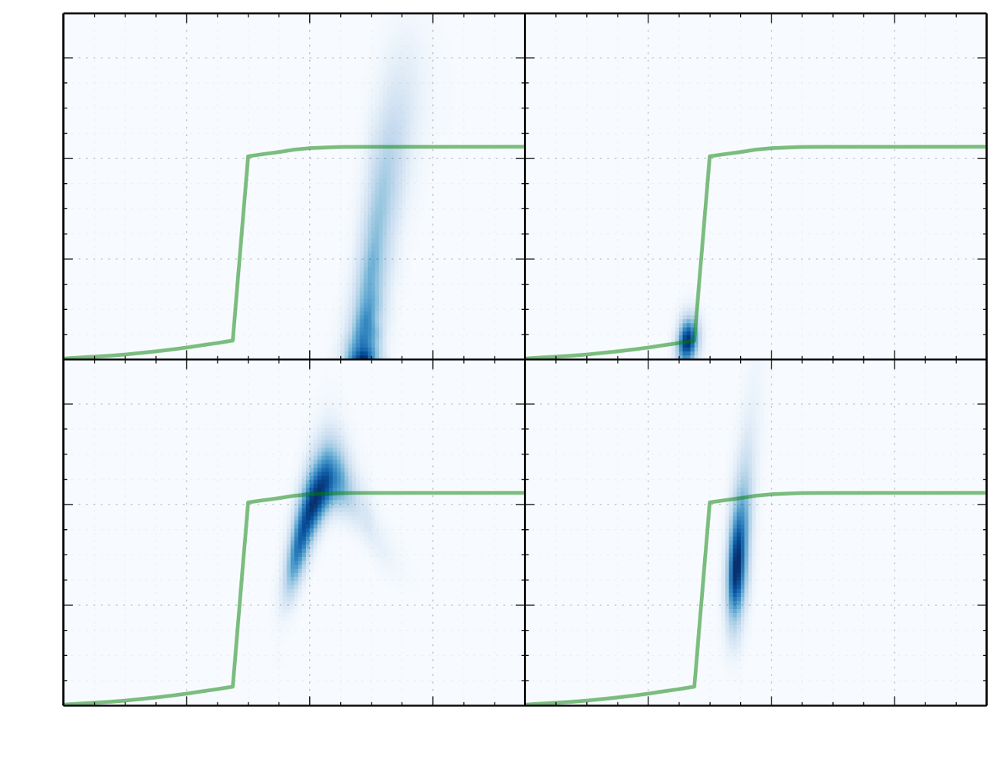
Mathematically equivalent to parameterization shown earlier.

Each star puts a constraint on the line-of-sight reddening.

Hundreds of stars per sightline.

Result for one pixel

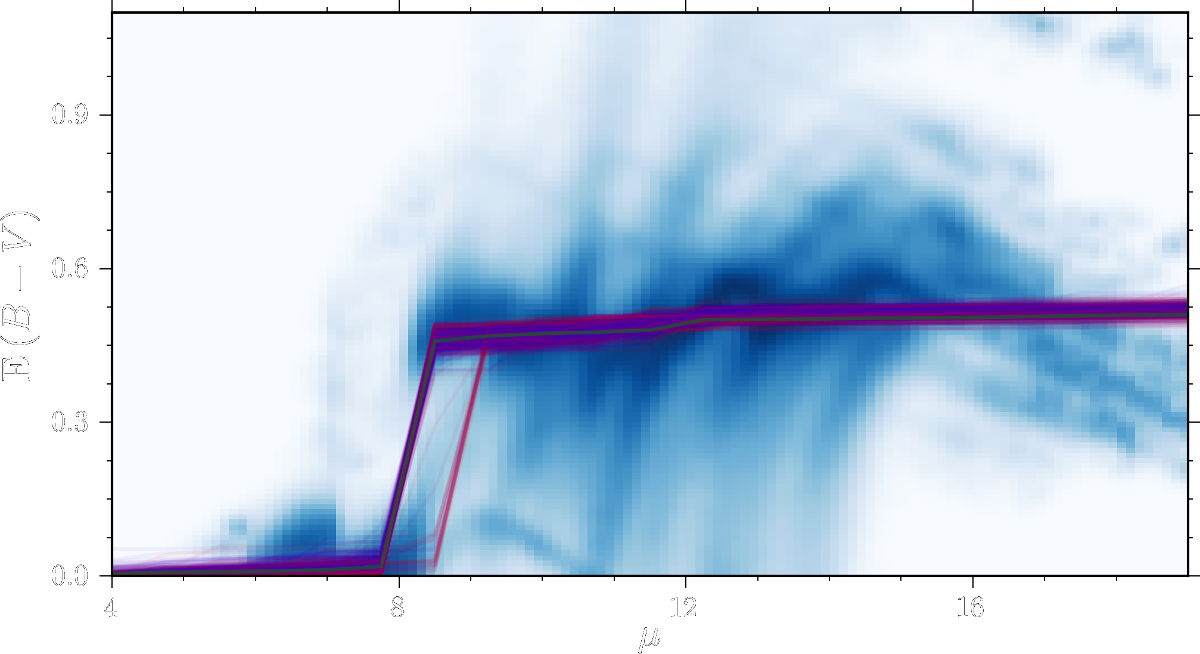
Result for Three Quarters of the Sky

Integrated Reddening:

Galactic anticenter

Looking towards the Galactic anticenter

50 pc orbit about the Sun

Cross-Sightline Correlations

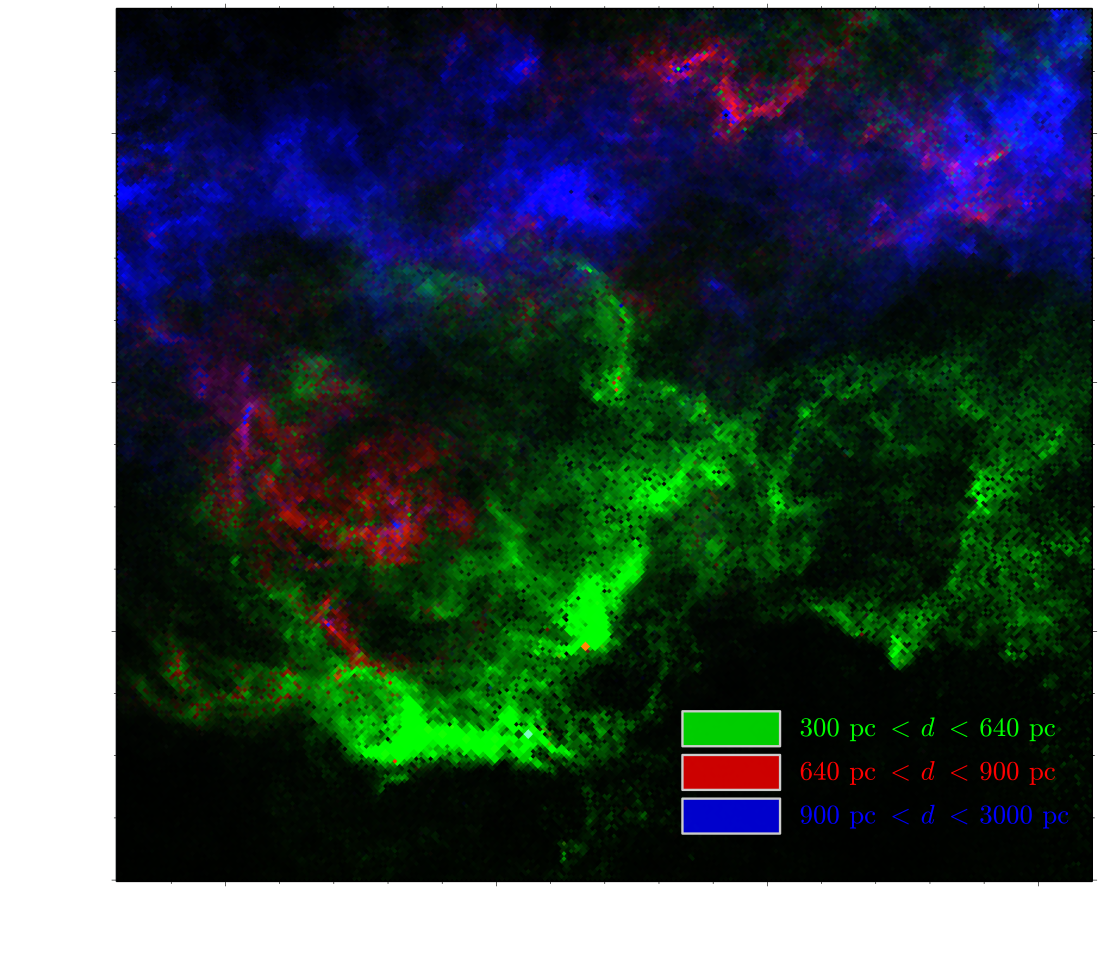
The cross-sightline differences in the above map are not a priori likely.

Cross-Sightline Correlations

Should include correlations between dust in neighboring sightlines, assuming some dust density power spectrum.
Couples stellar reddenings across the sky.
Since information is shared naturally across sightlines, we could theoretically shrink sightlines arbitrarily without loss of information.
Computational difficulty of large, coupled problem.